Page 10 - Math Course 3 (Book 1)

Adding and Subtracting Linear Inequalities
Mo. 1

Lesson 1
Let’s Begin

KEY CONCEPTS:
1. Solve linear inequalities by using addition. Solve by Adding
2. Solve linear inequalities by using subtraction
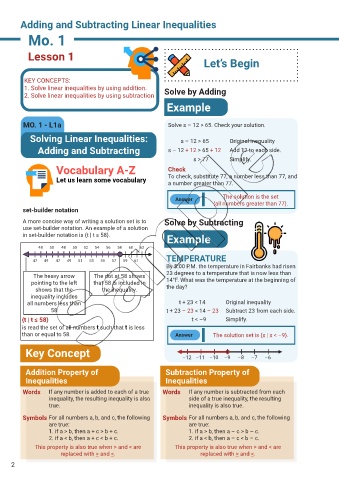
Example

MO. 1 - L1a Solve s – 12 > 65. Check your solution.

Solving Linear Inequalities: s – 12 > 65 Original inequality

Adding and Subtracting s – 12 + 12 > 65 + 12 Add 12 to each side.
s > 77 Simplify.
Vocabulary A-Z Check
Let us learn some vocabulary To check, substitute 77, a number less than 77, and
a number greater than 77.

Answer The solution is the set
{all numbers greater than 77}.
set-builder notation

A more concise way of writing a solution set is to Solve by Subtracting
use set-builder notation. An example of a solution
in set-builder notation is {t | t ≤ 58}.
Example
48 50 48 50 52 54 56 58 60 62
TEMPERATURE
47 49 47 49 51 53 55 57 59 61
By 5:00 P.M. the temperature in Fairbanks had risen
The heavy arrow The dot at 58 shows 23 degrees to a temperature that is now less than
pointing to the left that 58 is included in 14°F. What was the temperature at the beginning of
shows that the the inequality. the day?
inequality includes
all numbers less than t + 23 < 14 Original inequality
58 t + 23 – 23 < 14 – 23 Subtract 23 from each side.
{t | t ≤ 58} t < –9 Simplify.
is read the set of all numbers t such that t is less
than or equal to 58. Answer The solution set is {x | x < –9}.

Key Concept –12 –11 –10 –9 –8 –7 –6

Addition Property of Subtraction Property of
Inequalities Inequalities

Words If any number is added to each of a true Words If any number is subtracted from each
inequality, the resulting inequality is also side of a true inequality, the resulting
true. inequality is also true.

Symbols For all numbers a, b, and c, the following Symbols For all numbers a, b, and c, the following
are true: are true:
1. if a > b, then a + c > b + c. 1. if a > b, then a – c > b – c.
2. if a < b, then a + c < b + c. 2. if a < b, then a – c < b – c.
This property is also true when > and < are This property is also true when > and < are
replaced with > and <. replaced with > and <.
2