Page 64 - Math Course 2 (Book 2)

Congruent Angels in Parallel Lines

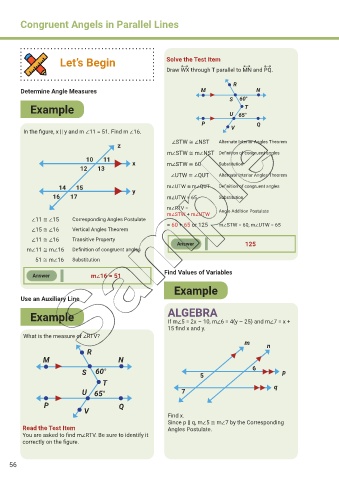
Let’s Begin Solve the Test Item
↔
↔
↔
Draw WX through T parallel to MN and PQ.
R
Determine Angle Measures M N
S 60°
Example U 65° T

P Q
In the figure, x || y and m ∠11 = 51. Find m ∠16. V
∠STW ≅ ∠NST Alternate Interior Angles Theorem
z
m∠STW ≅ m∠NST Definition of congruent angles
10 11 x
12 13 m∠STW ≅ 60 Substitution
∠UTW ≅ ∠QUT Alternate Interior Angles Theorem
14 15 y m∠UTW ≅ m∠QUT Definition of congruent angles
16 17 m∠UTW = 65 Substitution

m∠RTV = Angle Addition Postulate
m∠STW + m∠UTW
∠11 ≅ ∠15 Corresponding Angles Postulate
= 60 + 65 or 125 m∠STW = 60, m∠UTW = 65
∠15 ≅ ∠16 Vertical Angles Theorem

∠11 ≅ ∠16 Transitive Property
Answer 125
m∠11 ≅ m∠16 Definition of congruent angles
51 ≅ m∠16 Substitution

Find Values of Variables
Answer m∠16 = 51
Example
Use an Auxiliary Line

Example ALGEBRA
If m∠5 = 2x – 10, m∠6 = 4(y – 25) and m∠7 = x +
15 find x and y.
What is the measure of ∠RTV?
m n
R
M N
S 60° 5 6 p

T q
U 65° 7

P Q
V
Find x.
Since p || q, m∠5 ≅ m∠7 by the Corresponding
Read the Test Item Angles Postulate.
You are asked to find m∠RTV. Be sure to identify it
correctly on the figure.

56