Page 74 - Math Course 2 (Book 2)

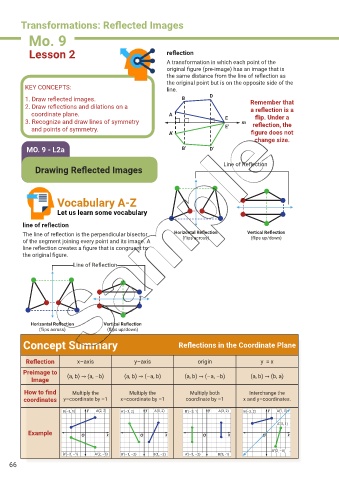
Transformations: Reflected Images

Mo. 9

Lesson 2 reflection

A transformation in which each point of the
original figure (pre-image) has an image that is
the same distance from the line of reflection as
the original point but is on the opposite side of the
KEY CONCEPTS: line.

1. Draw reflected images. B D Remember that
2. Draw reflections and dilations on a a reflection is a
coordinate plane. A E flip. Under a
3. Recognize and draw lines of symmetry m reflection, the
and points of symmetry. E’
A’ figure does not
change size.
MO. 9 - L2a B’ D’

Line of Reflection
Drawing Reflected Images

Vocabulary A-Z

Let us learn some vocabulary
line of reflection
The line of reflection is the perpendicular bisector Horizontal Reflection Vertical Reflection
(flips up/down)
(flips across)
of the segment joining every point and its image. A
line reflection creates a figure that is congruent to
the original figure.
Line of Reflection

Horizontal Reflection Vertical Reflection
(flips across) (flips up/down)
Concept Summary Reflections in the Coordinate Plane

Reflection x–axis y–axis origin y = x

Preimage to
Image (a, b) → (a, –b) (a, b) → (–a, b) (a, b) → (–a, –b) (a, b) → (b, a)

How to find Multiply the Multiply the Multiply both Interchange the
coordinates y–coordinate by –1 x–coordinate by –1 coordinate by –1 x and y–coordinates.

B(–3, 1) A(2, 3) A’(–3, 2) A(3, 2) B’(–3, 1) A(3, 2) B(–3, 2) A(1, 3)
A’(3, 1)
Example

B’(2, –3)
B’(–3, –1) A’(2, –3) B’(–1, –2) B(1, –2) A’(–3, –2) B(3, -1)
66