Page 76 - Math Course 2 (Book 2)

Transformations: Reflected Images

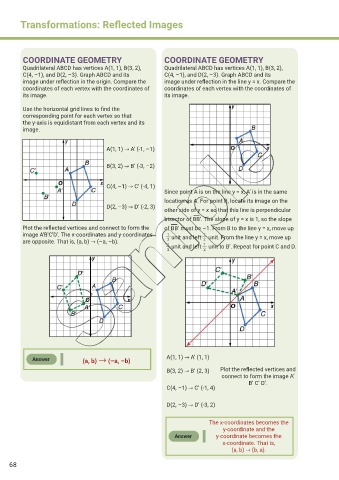
COORDINATE GEOMETRY COORDINATE GEOMETRY

Quadrilateral ABCD has vertices A(1, 1), B(3, 2), Quadrilateral ABCD has vertices A(1, 1), B(3, 2),
C(4, –1), and D(2, –3). Graph ABCD and its C(4, –1), and D(2, –3). Graph ABCD and its
image under reflection in the origin. Compare the image under reflection in the line y = x. Compare the
coordinates of each vertex with the coordinates of coordinates of each vertex with the coordinates of
its image. its image.

Use the horizontal grid lines to find the
corresponding point for each vertex so that
the y-axis is equidistant from each vertex and its
image.

A(1, 1) → A’ (-1, –1)

B(3, 2) → B’ (-3, –2)

C(4, –1) → C’ (-4, 1)
Since point A is on the line y = x, A’ is in the same
location as A. For point B, locate its image on the
D(2, –3) → D’ (-2, 3)
other side of y = x so that this line is perpendicular
bisector of BB’. The slope of y = x is 1, so the slope
Plot the reflected vertices and connect to form the of BB’ must be –1. From B to the line y = x, move up
image A'B'C'D'. The x-coordinates and y-coordinates unit and left unit. From the line y = x, move up
1
1
are opposite. That is, (a, b) → (–a, –b). 2 2
1
1
unit and left unit to B’. Repeat for point C and D.
2
2

Answer (a, b) → (–a, –b) A(1, 1) → A’ (1, 1)
B(3, 2) → B’ (2, 3) Plot the reflected vertices and
connect to form the image A’
B’ C’ D’.
C(4, –1) → C’ (-1, 4)

D(2, –3) → D’ (-3, 2)

The x-coordinates becomes the
y-coordinate and the
Answer y-coordinate becomes the
x-coordinate. That is,
(a, b) → (b, a).

68