Page 60 - Math Course 3 (Book 1)

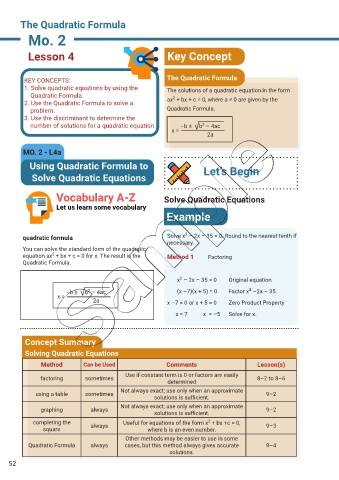
The Quadratic Formula
Mo. 2

Lesson 4 Key Concept

KEY CONCEPTS: The Quadratic Formula
1. Solve quadratic equations by using the The solutions of a quadratic equation in the form
Quadratic Formula. 2
2. Use the Quadratic Formula to solve a ax + bx + c = 0, where a ≠ 0 are given by the
problem. Quadratic Formula.
3. Use the discriminant to determine the
number of solutions for a quadratic equation. –b ± b – 4ac
2
x =
2a
MO. 2 - L4a

Using Quadratic Formula to Let’s Begin

Solve Quadratic Equations

Vocabulary A-Z Solve Quadratic Equations
Let us learn some vocabulary
Example

2
quadratic formula Solve x – 2x – 35 = 0. Round to the nearest tenth if
necessary.
You can solve the standard form of the quadratic
2
equation ax + bx + c = 0 for x. The result is the Method 1 Factoring
Quadratic Formula.

2
x – 2x – 35 = 0 Original equation
2
–b ± b – 4ac (x –7)(x + 5) = 0 Factor x² –2x – 35.
x =
2a x –7 = 0 or x + 5 = 0 Zero Product Property
x = 7 x = –5 Solve for x.

Concept Summary
Solving Quadratic Equations

Method Can be Used Comments Lesson(s)
Use if constant term is 0 or factors are easily
factoring sometimes 8–2 to 8–6
determined
Not always exact; use only when an approximate
using a table sometimes 9–2
solutions is sufficient.
Not always exact; use only when an approximate
graphing always 9–2
solutions is sufficient.
completing the always Useful for equations of the form x + bx +c = 0, 9–3
2
square where b is an even number.
Other methods may be easier to use in some
Quadratic Formula always cases, but this method always gives accurate 9–4
solutions.
52