Page 134 - Math Course 1 (Book 2)

Area: Triangles, Rhombi, And Trapezoids

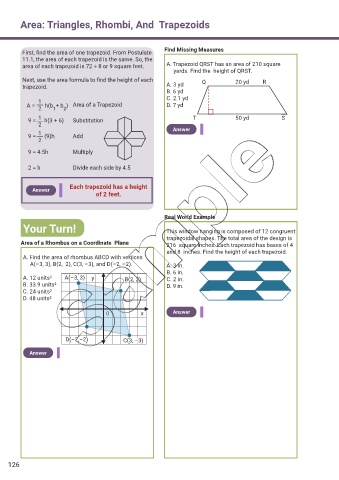
Find Missing Measures
First, f nd the area of one trapezoid. From Postulate
11.1, the area of each trapezoid is the same. So, the
area of each trapezoid is 72 ÷ 8 or 9 square feet. A. Trapezoid QRST has an area of 210 square
yards. Find the height of QRST.
Next, use the area formula to f nd the height of each Q 20 yd R
trapezoid. A. 3 yd
B. 6 yd
C. 2.1 yd
1
A = h(b + b ) Area of a Trapezoid D. 7 yd
2 1 2
1
9 = h(3 + 6) Substitution T 50 yd S
2
Answer
1
9 = (9)h Add
2
9 = 4.5h Multiply

2 = h Divide each side by 4.5

Each trapezoid has a height
Answer
of 2 feet.

Real World Example
Your Turn! This window hanging is composed of 12 congruent

trapezoidal shapes. The total area of the design is
Area of a Rhombus on a Coordinate Plane 216 square inches. Each trapezoid has bases of 4
and 8 inches. Find the height of each trapezoid.
A. Find the area of rhombus ABCD with vertices
A(–3, 3), B(2, 2), C(3, –3), and D(–2, –2). A. 3 in.
B. 6 in.
A. 12 units² A(–3, 3) y B(2, 2) C. 2 in.
B. 33.9 units² D. 9 in.
C. 24 units²
D. 48 units²

0 x Answer

D(–2,–2) C(3, –3)

Answer

126