Page 53 - Math Course 2 (Book 2)

Parallel and Perpendicular Lines

1 Subtract 2 from each
y + 2 –2 = x – 2 – 2 side. Your Turn!
2
1
y = x – 4 Write the equation in Parallel Line Through a Given Point
2 slope-intercept form.
Write the slope-intercept form of an equation for
1
Answer The equation is y = x 4 the line that passes through (2, 3) and is parallel to
2 1
the graph of y = 2 x – 1

Determine Whether Lines are Perpendicular
A. y = –2x + 3
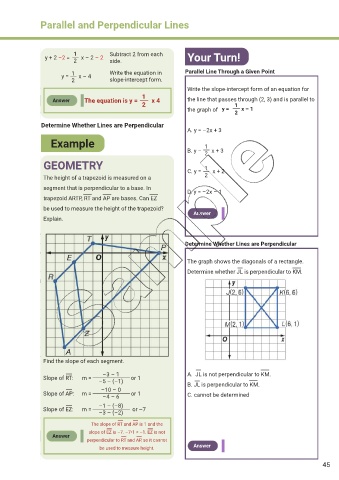
Example 1
B. y – x + 3
2
GEOMETRY
1
C. y = x + 2
The height of a trapezoid is measured on a 2
segment that is perpendicular to a base. In
D. y = –2x – 1
trapezoid ARTP, RT and AP are bases. Can EZ
be used to measure the height of the trapezoid?
Answer
Explain.

Determine Whether Lines are Perpendicular

The graph shows the diagonals of a rectangle.

Determine whether JL is perpendicular to KM.

Find the slope of each segment.

–3 – 1 A. JL is not perpendicular to KM.
Slope of RT: m = or 1
–5 – (–1) B. JL is perpendicular to KM.
–10 – 0
Slope of AP: m = or 1 C. cannot be determined
–4 – 6
–1 – (–8)
Slope of EZ: m = or –7
–3 – (–2)
The slope of RT and AP is 1 and the
slope of EZ is –7. –7•1 ≠ –1. EZ is not
Answer
perpendicular to RT and AP, so it cannot
be used to measure height. Answer

45